Diaporama Une approche différentielles du... calcul différentiel d'une conférence (courte) que j'ai donnée lors du 62e congrès de l'association mathématique du Québec.
Catégorie : Mathématiques
Problème de math (et standalone)
Je viens de découvrir le package LaTeX standalone (disponible dans TeXlive) qui permet de générer des images png comme celle-ci. Standalone utilise de manière transparente Imagemagick, l'outil graphique à tout faire.
Spirale d’Ulam
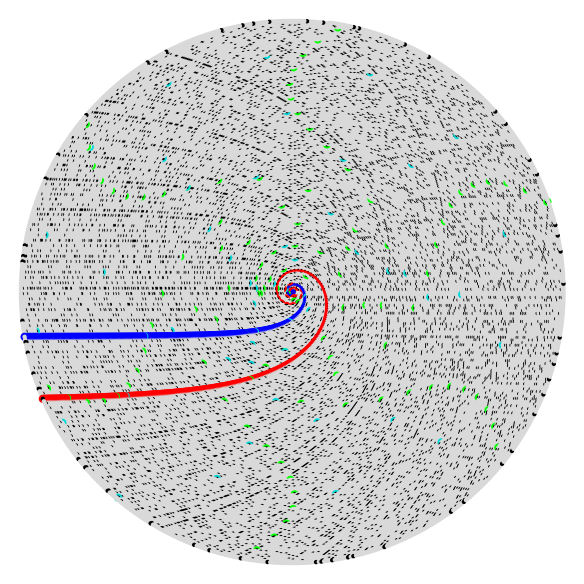
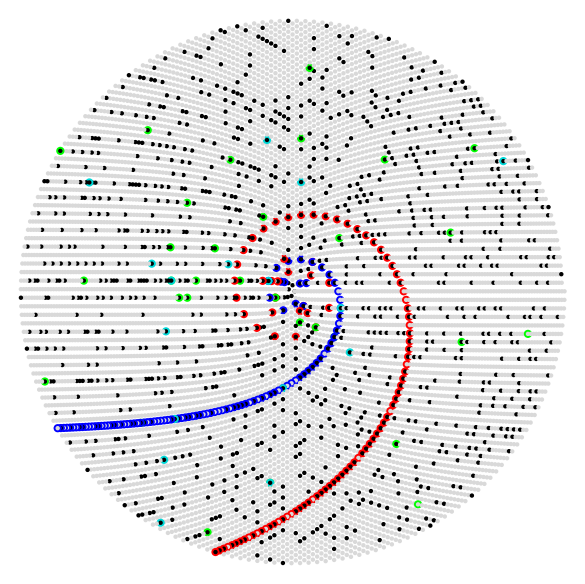
Images produites à l'aide de Sage. Elle montre comment se répartissent les 100000 et 50000 premiers nombres premiers, ainsi que quelques polynômes générateurs de nombres premiers.
Spirale d'Ulam sur Wikipedia.
Chronologie du développement des mathématiques
Première version publique de ma chronologie du développement des mathématiques.
Mathématiques en liberté
Mathématiques en liberté, La ville brûle, Montreuil, 2012.
Deux mathématiciens, Pierre Cartier qui fut l'un des piliers du fameux groupe Bourbaki et Cédric Villani, un des représentants les plus brillants de sa génération, le mathématicien et historien des sciences Jean Dhombres, et le philosophe des sciences Gerhard Heinzmann nous invitent à débattre avec eux de l'activité mathématique et de ses conséquences sociales, tant dans l'histoire de l'humanité que dans le monde contemporain.
Trois grandes directions ont été explorées par les auteurs dans leur dialogue :
- la relation, très complexe et objet de discussions et points de vue opposés, entre les mathématiques et la réalité ;
- la liberté que la construction des mathématiques a donné aux hommes en leur permettant de développer les sciences de la nature, mais aussi celle dont les mathématiciens ont besoin pour développer leurs recherches ;
- la responsabilité avec laquelle la communauté scientifique et les gouvernements doivent traiter la question de la place des mathématiques dans la politique de recherche et l'enseignement.
Game semantics for quantum data
Vidéo d'une conférence que j'ai donné lors du congrès Quantum Physics and Logic 2008 à l'Université de Reykjavik.
Ryoji Ikeda — systematics et datamatics
Page de l'exposition à la fondation DHC/ART : http://dhc-art.org/fr/exhibitions/ryoki-ikeda
Problèmes de mathématiques
Ah! les sondages: Et les méthodologies ont-elles eu un impact?
Claire Durand. “Ah! Les Sondages: Et Les Méthodologies Ont-elles Eu Un Impact?” Ah ! Les Sondages, May 3, 2011. http://ahlessondages.blogspot.ca/2011/05/et-les-methodologies-ont-elles-eu-un.html.
Claire Durand. Et les méthodologies ont-elles eu un impact ? Blog: Ah ! Les Sondages, 3 mai 2011.
Mathjax
[mathjax]
Mathjax est un projet libre de librarie javascript soutenu financièrement par plusieurs organismes et éditeurs importants en mathématiques afin de pouvoir afficher facilement du contenu mathématique de haute qualité sur web. Je l'utilise maintenant sur mon site personnel, mon site pour mes étudiants et bien sur pour ce carnet. Le rendu typographique est très beau, et peut être « zoomé ». Voici par exemple les deux parties du théoreme fondamental du calcul:
$$\frac{d}{dx}\int_a^x f(t)\,dt = f(x)$$
$$\int_a^b f'(x)\,dx = f(b)-f(a)$$
Pour utiliser mathjax, on peut simplement ajouter un peu de code dans l'entête html, ce qui aura pour effet de charger la librairie à partir du serveur central du projet. Cette méthode a l'avantage de ne pas exiger l'installation locale de mathjax.